Hamming Distance

发表于 | 分类于 | | 热度: ℃
字数统计: 3,486 | 阅读时长 ≈ 15

0x00 引例

From : Problem Address

题目描述: 该题目给出来一长串密文,现在已知该密文是由明文按密钥长度分组后与同一密钥进行异或得到的,需要从密文还原得到明文.

类型: 流密码密钥重用.

0x01 汉明距离

所谓汉明距离,是在二进制层面观测两个等长字符串的比特位差异,比如: 

1
2
3
hamming("1010","1011") == 1
hamming("1111","0000") == 4
hamming("1111","1111") == 0

可见,1010与1011有一个比特位存在差异,所以汉明距离为1.对于两个比特串,有一个快速的方法求解汉明距离:根据0 xor 1 == 1 和 0 xor 0 == 0,可以将两个比特串进行异或然后计算值为1的比特位的个数,就是最后的汉明距离.
简单实现代码:

hamming_distance = bint(bytes1 ^ bytes2).count("1")

汉明距离可以应用于数据相似度的量化,面部识别以及指纹识别等特征数据识别都可以运用到汉明距离来进行数据量化.

Leetcode刷题:

191.Number of 1 Bits

461.Hamming Distance

477.Total Hamming Distance

0x02 攻击细节

对于此类流密码重用的题目,我们首先明确思路:第一步,找到进行加密的密钥长度;第二步,通过特定的方法还原出密钥内容;第三步,通过异或得到明文.

下面我们分别进行分析.

0x03 寻找密钥长度

我们首先想到使用爆破来求解密钥长度,但发现随着密钥长度的增加,暴力破解的方法效率十分低下,于是出现了使用汉明距离来求解的方法.具体的汉明距离求解代码如下: 

1
2
3
4
5
6
7
8
9
10
11
def bxor(a,b): #取字符串等长部分进行异或
	if len(a) > len(b):
		return bytes([x ^ y for x, y in zip(a[: len(b)], b)]) #将字符串转换成比特流
	else:
		return bytes([x ^ y for x, y in zip(a, b[: len(a)])])
		
def hamming_distance(bit1,bit2):  #计算两个字符的汉明距离
	result = 0
	for byte in bxor(bit1, bit2):
		result += bin(byte).count("1")
	return result

通过扩展资料,我们可以知道,两个以ascii编码的英文字符的汉明距离是2-3之间,也就是说正常英文字母的平均汉明距离为2-3(每比特),任意字符(非纯字母)的两两汉明距离平均为4.另外,正确分组的密文和密文之间的汉明距离等于对应明文与明文之间的汉明距离.这样,当使用正确的密钥长度后,两两字母进行计算汉明距离,那么这个值应该是趋于最小.我们前几对分组取出计算平均汉明距离,将结果列出.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
import base64

def bxor(a,b):
	if len(a) > len(b):
		return bytes([x ^ y for x, y in zip(a[: len(b)], b)]) #将字符串转换成比特流
	else:
		return bytes([x ^ y for x, y in zip(a, b[: len(a)])])


def hamming_distance(bit1,bit2):  #计算两个字符的汉明距离
	result = 0
	for byte in bxor(bit1, bit2):
		result += bin(byte).count("1")
	return result


text = ""
with open("problem1", "r") as f:
	for line in f:
		text += line
tmp = base64.b64decode(text)

average_distances = []

for KEYSIZE in range(2,40): #爆破密钥key的长度,从2到40依次列出

	tmp1 = tmp[: KEYSIZE]
	tmp2 = tmp[KEYSIZE: KEYSIZE * 2]
	tmp3 = tmp[KEYSIZE * 2: KEYSIZE * 3]
	tmp4 = tmp[KEYSIZE * 3: KEYSIZE * 4]
	tmp5 = tmp[KEYSIZE * 4: KEYSIZE * 5]
	tmp6 = tmp[KEYSIZE * 5: KEYSIZE * 6]
	
	#计算前六段的平均汉明距离
	
	average_distance = float(
	hamming_distance(tmp1, tmp2) +
	hamming_distance(tmp2, tmp3) +
	hamming_distance(tmp3, tmp4) +
	hamming_distance(tmp4, tmp5) +
	hamming_distance(tmp5, tmp6)
	) / (KEYSIZE * 5)

	average_distances.append((KEYSIZE, average_distance))
	
#key是sorted函数进行排序所遵从的规则,lambda函数使得排序按照average_distance从小到大进行排序

average_distances = sorted(average_distances,key = lambda x: x[1])
print(average_distances)

结果如下:

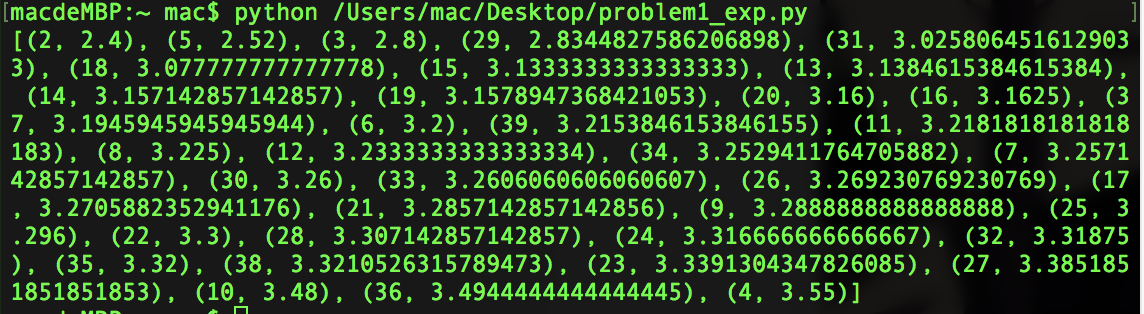
hamming_result.png-294kB
计算出汉明距离后我们可以取前几个密钥长度来进行爆破求解,缩小爆破范围,提高效率.

0x04 爆破得到密钥

密钥获得过程中,有两个行之有效的方法.

Method 1 利用明文空格

我们使用了异或的定律和一个技巧:

1
2
异或定律: c1 xor c2 == p1 xor p2 (p1 = c1 xor K, p2 = c2 xor K)  
技巧:空格和所有小写字母的异或结果为对应的大写字母,和所有大写字母的异或结果为对应的小写字母

该技巧可以使用以下的脚本进行验证: 

1
2
3
value = 'abcdefghijklmnopqrstuvwxyzABCDEFGHIJKLMNOPQRSTUVWXYZ'
for asc1 in value:
    print(asc1,"^0x20---->",chr(ord(asc1)^0x20))

这样当两个密文按照字节异或后的结果处于字母表的ascii值之间,有很大的概率对应相异或的明文之一为空格,那么根据这个规律,我们可以依次遍历出密钥的每个字节,当捕获的密文组足够多的时候,我们有很大概率得到每个密钥对应异或的字节上的明文为空格,然后依次异或出密钥.

当然,这里有一个问题,如果说两个字母相异或是否也有可能产生ascii码范围内的字符呢?答案是可能的,但是如果一个字符和某一分组中所有的密文相异或的结果都是ascii码字符,我们可以判断该字符一定是空格.

这样我们的任务就非常简单了,将按照爆破的密钥长度进行分组后,每一组对应位置的字符进行重组分组,保证新形成的组别中所有的字符都是对应明文与同一个密钥字符异或的结果.接下来,我们的任务就变成了在新组别中找到明文为空格的位置,我们使用循环嵌套,将新组别中的每一个字符与该组中其他字符异或,结果中含有最多ascii码范围内字符的原始字符最有可能为空格,记录该位置,将该位置对应的密文与空格进行异或,从而得到密钥.

关键部分的证明: 

1
2
3
4
5
since c1 xor c2 == p1 xor p2 and p1 == c1 xor k,p2 == c2 xor k.

if c1 == 0x20,then c1 xor k == p1,

so k == c1 xor p1,that is k == p1 xor 0x20

以下是具体步骤: 

1
2
3
4
1. 使用取模运算把密文分成n个分组（其中n是密钥长度），如此以来，我们就有了n个独立的凯撒加密式的密文组（因为每个分组里面的值是使用同一个密钥字节明文异或）。这样就把问题简化成了破解n个独立的凯撒加密模式的单字节抑或密码方式。这一步可以直接使用爆破，但是效率不高。我们采取另一种姿势。
2. 将2中的每个分组做如下的操作：每个分组做嵌套循环，内循环，外循环。设置外循环计数值possible_space=0，max_possible=0，设置内循环计数值maxpossible=0,依次取出每个分组中的每一个字节做与其他字节两两抑或进行内循环，如果结果是字母，我们就把内循环计数值maxpossible+1,在每个内循环结束后进行max_possible的更新（与内循环maxpossible做对比），并记录当前字节的位置到possible_space，然后外循环继续。直至遍历完所有的字节。取出max_possible对应的字节位置possible_space处的字节码，我们把它对应的明文假设成空格（根据之前的讨论）然后将该位置的字节和0x20（空格）异或;找出相应位置的密钥字节。
3. 重复2中的步骤，依次根据每个分组找出每位的密钥字节，至此密钥破解完毕
4. 将找出的密钥用于破解密文。当密文足够多，可以发现破解的准确率很高，基本可以做到无差别破解。

使用汉明距离的改进版破解代码(KEYSIZE不需要从2开始一直爆破到40,而是只取汉明距离最小的前5种情况)如下: 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
import base64
import string

def bxor(a,b):   #异或两个长度不同的比特串
	if len(a) > len(b):
		return bytes([x ^ y for x, y in zip(a[:len(b)], b)])
	else:
		return bytes([x ^ y for x, y in zip(a, b[:len(a)])])


def hamming_distance(b1,b2):
	result = 0
	for byte in bxor(b1,b2):
		result += bin(byte).count("1")
	return result


def break_single_key_xor(text):
	key = 0
	possible_space = 0
	max_possible = 0
	letters = string.ascii_letters.encode('ascii') #相当于所有可显示的ascii字符构成的字符集
	for a in range(0, len(text)):
		maxpossible = 0
		for b in range(0, len(text)):
			if(a == b):
				continue
			c = text[a] ^ text[b]
			if c not in letters and c != 0 :
				continue
			maxpossible += 1
		if maxpossible > max_possible:  #由c1 xor c2 == p1 xor p2 与其他字符异或结果为字母最多的位置其明文最可能是空格
			max_possible = maxpossible
			possible_space = a
	key = text[possible_space] ^ 0x20  #将密文与空格异或从而得到密钥的ascii
	return chr(key)


text = ''
with open('problem1', 'r') as f:
	for line in f:
		text += line

tmp = base64.b64decode(text)

average_distances = []

for KEYSIZE in range(2,40): #爆破密钥key的长度
	
	tmp1 = tmp[: KEYSIZE]
	tmp2 = tmp[KEYSIZE: KEYSIZE * 2]
	tmp3 = tmp[KEYSIZE * 2: KEYSIZE * 3]
	tmp4 = tmp[KEYSIZE * 3: KEYSIZE * 4]
	tmp5 = tmp[KEYSIZE * 4: KEYSIZE * 5]
	tmp6 = tmp[KEYSIZE * 5: KEYSIZE * 6]
	
	#计算前六段的平均汉明距离
	
	average_distance = float(
	hamming_distance(tmp1, tmp2) +
	hamming_distance(tmp2, tmp3) +
	hamming_distance(tmp3, tmp4) +
	hamming_distance(tmp4, tmp5) +
	hamming_distance(tmp5, tmp6)
	) / (KEYSIZE * 5)

	average_distances.append((KEYSIZE, average_distance))
	
#key是sorted函数进行排序所遵从的规则,lambda函数使得排序按照average_distance从小到大进行排序

average_distances = sorted(average_distances,key = lambda x: x[1])


for KEYSIZE,_ in average_distances[:5]:
	block_bytes = [[] for _ in range(KEYSIZE)] #建立KEYSIZE大小的列表
	for i, byte in enumerate(tmp):
		block_bytes[i % KEYSIZE].append(byte) #i % KEYSIZE从而保证相同位置的分到一组
	keys =""
	try:
		for bbytes in block_bytes:
			keys += break_single_key_xor(bbytes)
		key = bytearray(keys * len(tmp), "utf-8")  #bytearray方法将字符串key转换成比特流
		plaintext = bxor(tmp, key)  #重新异或一遍得到明文比特流
		print("keysize:", KEYSIZE)
		print("key is:", keys, "n")
		s = bytes.decode(plaintext)  #进行解密得到明文
		print(s)
	except Exception:
		continue

我们发现,输出结果中,当KEYSIZE为29时,破解出的文字为有意义的英文文本即明文.

Method 2 字频分析

我们可以使用字频来进行分析,即利用字母出现频率的统计规律进行权重赋值,当总权重最高时,我们有理由相信这时的密钥字节是正确的.先贴上解题代码: 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
import base64
import string


def bxor(a, b):     # xor two byte strings of different lengths
    if len(a) > len(b):
        return bytes([x ^ y for x, y in zip(a[:len(b)], b)])
    else:
        return bytes([x ^ y for x, y in zip(a, b[:len(a)])])


def hamming_distance(b1, b2):
    differing_bits = 0
    for byte in bxor(b1, b2):
        differing_bits += bin(byte).count("1")
    return differing_bits


def score(s):
    freq = {}
    freq[' '] = 700000000
    freq['e'] = 390395169
    freq['t'] = 282039486
    freq['a'] = 248362256
    freq['o'] = 235661502
    freq['i'] = 214822972
    freq['n'] = 214319386
    freq['s'] = 196844692
    freq['h'] = 193607737
    freq['r'] = 184990759
    freq['d'] = 134044565
    freq['l'] = 125951672
    freq['u'] = 88219598
    freq['c'] = 79962026
    freq['m'] = 79502870
    freq['f'] = 72967175
    freq['w'] = 69069021
    freq['g'] = 61549736
    freq['y'] = 59010696
    freq['p'] = 55746578
    freq['b'] = 47673928
    freq['v'] = 30476191
    freq['k'] = 22969448
    freq['x'] = 5574077
    freq['j'] = 4507165
    freq['q'] = 3649838
    freq['z'] = 2456495
    score = 0
    string=bytes.decode(s)
    for c in string.lower():
        if c in freq:
            score += freq[c]
    return score


def break_single_key_xor(b1):
    max_score = 0
    english_plaintext = 0
    key = 0

    for i in range(0,256):
        b2 = [i] * len(b1)
        try:
            plaintext = bxor(b1, b2)
            pscore = score(plaintext)
        except Exception:
            continue
        if pscore > max_score or not max_score:
            max_score = pscore
            english_plaintext = plaintext
            key = chr(i)
    return key



text = ''
with open("problem1", "r") as f:
    for line in f:
        text += line
b = base64.b64decode(text)


normalized_distances = []


for KEYSIZE in range(2, 40):
    # 我们取其中前6段计算平局汉明距离
    b1 = b[: KEYSIZE]
    b2 = b[KEYSIZE: KEYSIZE * 2]
    b3 = b[KEYSIZE * 2: KEYSIZE * 3]
    b4 = b[KEYSIZE * 3: KEYSIZE * 4]
    b5 = b[KEYSIZE * 4: KEYSIZE * 5]
    b6 = b[KEYSIZE * 5: KEYSIZE * 6]
    b7 = b[KEYSIZE * 6: KEYSIZE * 7]

    normalized_distance = float(
        hamming_distance(b1, b2) +
        hamming_distance(b2, b3) +
        hamming_distance(b3, b4) +
        hamming_distance(b4, b5) +
        hamming_distance(b5, b6) 
    ) / (KEYSIZE * 5)
    normalized_distances.append(
        (KEYSIZE, normalized_distance)
    )
normalized_distances = sorted(normalized_distances, key=lambda x: x[1])


for KEYSIZE, _ in normalized_distances[:5]:
    block_bytes = [[] for _ in range(KEYSIZE)]
    for i, byte in enumerate(b):
        block_bytes[i % KEYSIZE].append(byte)
    keys = ''

    for bbytes in block_bytes:
        keys += break_single_key_xor(bbytes)
    key = bytearray(keys * len(b), "utf-8")
    plaintext = bxor(b, key)
    print("keysize:", KEYSIZE)
    print("key is:", keys, "n")
    s = bytes.decode(plaintext)
    print(s)

0x05 总结

  • 关键词:汉明距离,流密码重用的不安全性.

  • 汉明距离用于判断数据的相似程度,可以通过简单的异或并统计”1”的个数来计算.

  • 异或加密中,明文和明文的异或等于密文和密文的异或,并且二者的汉明距离一样.

  • 空格(0x20)和所有小写字母异或结果为相应的大写字母,和所有大写字母异或的结果为相应的小写字母.

  • 两个以ascii编码的英文字符的汉明距离是2-3之间，也就是说正常英文字母的平均汉明距离为2-3（每比特），任意字符（非纯字母）的两两汉明距离平均为4.

  • 破解此类问题的方法:爆破密钥长度;分组与空格异或寻找密钥;将密钥与密文异或还原明文.其中运用汉明距离可以缩小爆破范围,提高运算效率.

请作者吃个小鱼饼干吧
分享到： 收藏夹 复制网址 邮件 微信 QQ空间 腾讯微博 豆瓣 一键分享 更多